Wright Access.

The Haskell gl package

a pragmatic primer

This post demonstrates how to get to a useful, working foundation for an OpenGL application using the recent gl package with the minimum of fuss. By the end of the post, this is what we’ll have:

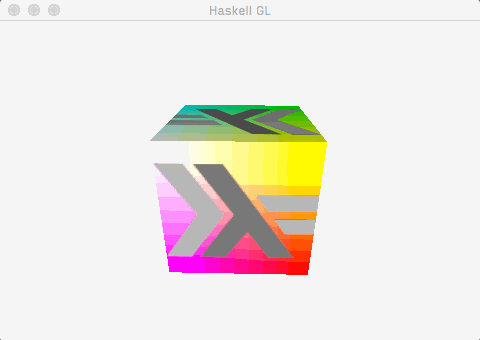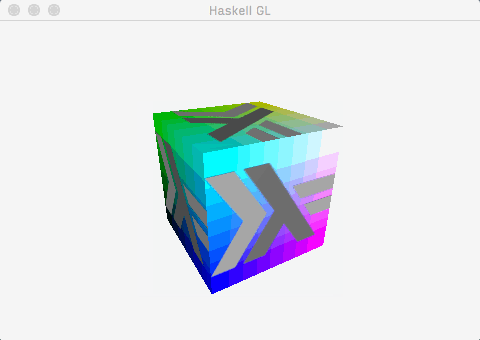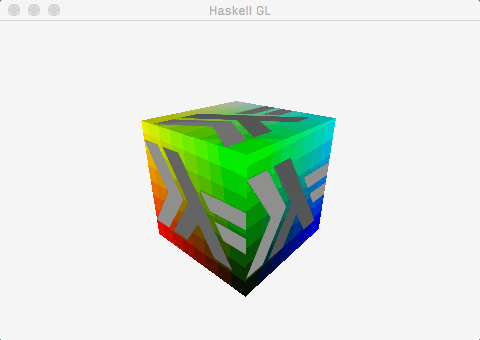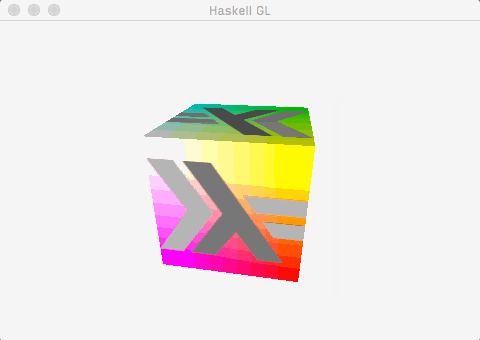
Which is to say:

• A window, created and managed by GLFW-b.
• A cube mesh, with positions, colours, normals, and uv co-ordinates.
• A single directional light, calculated using the fragment shader.
• A texture, alpha blended with the underlying colours.
• Some very simple animation (the cube spins).

When trying to get set up with OpenGL, I’ve found that while there are a lot of resources out there, I’ve often had to piece together various blog posts in order to get a working application that I can build off. Many of these blog posts also make use of immediate mode, which may be quick and easy to learn, but is quite outdated and ultimately sets you down the wrong path if you want to learn modern OpenGL programming. This post aims to give you a solid jumping-off point to start on the interesting stuff straight away.

As well as that, this post is an opportunity for me to try the gl package, introduced relatively recently by Edward Kmett and others. gl attempts to be a low-level but complete set of bindings to the OpenGL API – as opposed to the rather more longstanding OpenGL package, which tries to be a bit more “Haskelly” but at the cost of certain missing parts of the OpenGL specification.

To me, though, the greatest advantage of the gl package is that you can google it. Because it is machine-generated from the actual OpenGL API, all the symbol names match, and you use them in the same way as you would in C. The vast majority of OpenGL tutorials on the internet are written in C or C++, so having a common vocabulary with them is immensely useful.

Setting up the project

In case you want to follow along, here is the relevant part of my cabal file:

executable glTutorial

  main-is: 2015-03-25-the-haskell-gl-package.lhs

  build-depends:    

base                 

>= 4.7 && <4.8,

base-unicode-symbols

== 0.2.2.4,

transformers         

== 0.4.3.0,

vector               

== 0.10.12.2,

text                 

== 1.2.0.3,

gl                   

== 0.7.2.4,

GLFW-b               

== 1.4.7.1,

linear               

== 1.18.0.1,

distributive         

== 0.4.4,

lens                 

== 4.6.0.1,

JuicyPixels          

== 3.2.3

  default-language: 

Haskell2010

I am including absolute version numbers here so that you can see exactly what I was working with, but you could probably be a lot more lenient with your own projects.

This post is a literate Haskell file – lines preceded by > are executable code, so you should be able to run and test the file directly.

Breakdown of tasks

This post is, by necessity, quite long. There is a lot that needs to be set up in order to get a spinning cube on the screen! This is basically how I’ve started every games/graphics project I’ve done in the last ten years, and every time I spend the majority of my time staring into the abyss of a bright pink window with nothing rendering in it, wondering which trivial step I’ve forgotten in my initial setup which is breaking everything. By collecting all the steps together in this one, massive blog post, I hope to save others (as well as my future self) from this pain.

To help navigate, here’s a breakdown of what we’re going to be doing:

• Set up language pragmas / import the required modules
• Set up some handy error handling utilities
• Create a window and associate it with our GL context
• Define the mesh for our cube
• Load Resources:
  • Load in the texture and upload it to the GPU
  • Compile and link the shader, and retrieve its uniform and attribute locations
  • Convert our mesh definition to GL buffer objects
• Initialise OpenGL
• Update state every frame to rotate the cube
• Actually render the scene
• Cleanup

Let’s get started!

Preliminaries

We start with language pragmas. We will overload both string and list syntax to provide us with convenient access to Haskell’s faster Text and Vector containers.

> {-# LANGUAGE OverloadedStrings #-}

> {-# LANGUAGE OverloadedLists #-}

The gl package makes quite heavy use of pattern synonyms to reproduce GL’s native enums.

> {-# LANGUAGE PatternSynonyms #-}

I’m also going to make use of Unicode symbols in this file.

> {-# LANGUAGE UnicodeSyntax #-}

> import Prelude.Unicode

> import Control.Monad.Unicode

Obviously we’ll begin by importing the Graphics.GL namespace exposed by the gl package. This package follows the GL C API convention of prefixing its function names with gl, so I won’t bother with a qualified import; for all other modules I will either import them qualified or explicitly name the imported symbols, so that you can see where they’re coming from.

> import Graphics.GL

To make things easier, I’m going to make use of GLFW to deal with opening the window and getting keypresses. This will allow us to concentrate on the GL side of things.

> import qualified Graphics.UI.GLFW as GLFW

Edward Kmett’s linear library is a nice, flexible library for vector and matrix maths, and the Storable instances it supplies for everything make it a good fit for working with GL.

> import Linear (

V2(..), V3(..), M44, Quaternion,

>                

perspective, lookAt, axisAngle,

>                

mkTransformation, (!*!), inv33,

>                

column, _xyz, negated, identity)

The following two functions also come in handy when working with Linear. distribute gives you the transpose of a matrix, and (^.) will give you access to certain fields which are expressed as lenses.

> import Data.Distributive 

(distribute)

> import Control.Lens      

((^.))

I’m going to use the JuicyPixels library for loading texture data.

> import Codec.Picture 

(readPng, Image(Image),

>                      

DynamicImage(ImageRGBA8))

After this we import some standard libraries which we’ll be making use of later.

> import Control.Monad       

(

void, when, unless, liftM2)

> import Control.Applicative 

(

(<$>), (<*>), pure)

> import System.IO           

(

hSetBuffering, stdout,

>                            

BufferMode(LineBuffering))

> import Data.IORef          

(

IORef, newIORef,

>                            

writeIORef, readIORef)

> import Data.Bits           

(

(.|.))

We’ll be working with strings a little bit to load our shaders and send them into GL, so we’ll need Data.Text and the Data.Text.Foreign utilities for communicating with C. We’ll also include Data.Vector while we’re at it.

> import qualified Data.Text         

as T

> import qualified Data.Text.IO      

as T

> import qualified Data.Text.Foreign 

as T

> import qualified Data.Vector       

as V

Because gl works at quite a low level, you have to do quite a lot of marshalling between Haskell and C. Haskell provides a number of convenient utilities for doing this within the Foreign hierarchy. Data.Vector.Storable also gives us a directly serializable form of Vector.

> import qualified Data.Vector.Storable as SV

> import Foreign.Marshal.Alloc 

(alloca, allocaBytes)

> import Foreign.Marshal.Array 

(allocaArray, peekArray)

> import Foreign.Marshal.Utils 

(with)

> import Foreign.Storable      

(peek, sizeOf)

> import Foreign.Ptr           

(Ptr, nullPtr, castPtr, wordPtrToPtr)

Finally, some monad transformers which will ease some of the boilerplate.

> import Control.Monad.Trans.Maybe 

(MaybeT(..))

> import Control.Monad.Trans.Cont  

(ContT(..), evalContT)

> import Control.Monad.Trans.Class 

(lift)

> import Control.Monad.IO.Class    

(liftIO)

Error-handling utilities

I don’t actually make use of these functions anywhere within this post, but you can bet I used them while I was writing it! Debugging graphical issues can be extremely frustrating as the GPU doesn’t have anything akin to a printf, and GL itself is basically a gigantic state machine where subtle mistakes can lead to strange errors down the line. Sometimes it can be useful to take a scattergun approach and just sprinkle error-checking facilities throughout your code in the hope of getting a clue as to what might be the problem. These functions help you do that.

First, getErrors collects all the errors GL is currently reporting. Since GL allows certain operations to be performed concurrently, it holds multiple error registers, and a single call to glGetError just gives you the value from one of them. Here, we keep calling it until there are no errors left, at which point we return all the available errors as a list.

> getErrors :: IO [GLuint]

> getErrors = do

>   err ← glGetError

>   if err == GL_NO_ERROR

>      then return []

>      else do

>        errs ← getErrors

>        return $ err:errs

The errors themselves are, like most things in GL, just a GLuint that maps to some enumerated value. The documentation for glGetError gives us a clue as to what values might be returned, so we can use that to convert the errors to a more useful String value.

> showError :: GLuint → String

> showError GL_INVALID_ENUM =

>   "GL_INVALID_ENUM"

> showError GL_INVALID_VALUE =

>   "GL_INVALID_VALUE"

> showError GL_INVALID_OPERATION =

>   "GL_INVALID_OPERATION"

> showError GL_INVALID_FRAMEBUFFER_OPERATION =

>   "GL_INVALID_FRAMEBUFFER_OPERATION"

> showError GL_OUT_OF_MEMORY =

>   "GL_OUT_OF_MEMORY"

> showError GL_STACK_UNDERFLOW =

>   "GL_STACK_UNDERFLOW"

> showError GL_STACK_OVERFLOW =

>   "GL_STACK_OVERFLOW"

> showError x = "GL Error " ++ show x

Finally, printErrors is the function we’ll actually use. It uses the above two functions to collect the errors and output them. I found it useful just to crash straight away at these point, so I report the errors using error. If you wanted to try and continue despite the errors you could use putStrLn instead.

> printErrors :: String → IO ()

> printErrors prefix = do

>   es ← map showError <$> getErrors

>   when (not $ null es) $

>     error (prefix ++ ": " ++ show es)

Note the prefix parameter, which just lets you put in a little string describing where in the code the error occurred. Armed with this function, you can scatter error checks all over the place to help narrow down the cause of a problem to specific regions of code.

Setting up the window

The main function of our application begins by setting up the window using GLFW and binding it to our current GL context. Once that’s done, it can hand off to our initialisation and main loop to do the bulk of the work.

Because I want to keep the distinction between GLFW and OpenGL quite strong, I’ve chosen not to mix them up in this post. This section, which deals with window setup and initialisation, uses GLFW exclusively and makes no direct GL calls at all. Once this section is over, we won’t touch GLFW again and it will be pure GL from then on.

> main :: IO ()

> main = do

>   hSetBuffering stdout LineBuffering

Not strictly necessary, but I begin here by setting stdout to use LineBuffering. This means any output will be flushed on every newline, which can be invaluable for debugging.

Next, we need to initialise GLFW.

>   success ← GLFW.init

>   if not success

>   then void $ putStrLn "Failed to initialise GLFW"

>   else do

If GLFW won’t initialise we might as well give up, otherwise we can continue on into our program.

We need to provide GLFW with some hints to tell it how to set up the window. These will vary depending on the architecture you want to support.

>     mapM_ GLFW.windowHint

>       [ GLFW.WindowHint'ClientAPI

>           GLFW.ClientAPI'OpenGL

>       , GLFW.WindowHint'OpenGLProfile

>           GLFW.OpenGLProfile'Core

>       , GLFW.WindowHint'OpenGLForwardCompat True

>       , GLFW.WindowHint'ContextVersionMajor 3

>       , GLFW.WindowHint'ContextVersionMinor 2 ]

I’ve rather arbitrarily opted for OpenGL 3.2 here, which is not outrageously out-of-date but is still widely supported. More information about the available window hints can be found in the GLFW documentation.

We’re now ready to make the window. Again, it’s possible this may fail, so we’ll just drop out with an error if that happens.

>     w ← 

GLFW.createWindow 480 320 "Haskell GL"

>         

Nothing Nothing

>     case w of

>       Nothing  

→ putStrLn "Failed to create window"

>       Just win 

→ do

OK, we have a window! First things first, let’s associate the current GL context with this window so that any GL calls we make from now on will apply to it.

>         GLFW.makeContextCurrent w

The next step is to hook into GLFW’s callbacks. In reality, I don’t think the GLFW design of responding to callbacks fits the Haskell mindset very well as you necessarily have to have callbacks modify some sort of global state, but since we’re using GLFW we’re stuck with it. For a serious game project I would probably just do the window handling myself and take a different approach.

So, we start off by setting up handling of the “close” button. We create an IORef to tell us whether the window has been closed, which we set to True when the close button is pressed. That way we can check at any time during our game loop whether we need to shut down. We could also close the window on a keypress simply by setting the same IORef value. It’s quick and dirty, but it works:

>         closed ← newIORef False

>         GLFW.setWindowCloseCallback win $

>           Just (const $ writeIORef closed True)

We’ll also want to hook into GLFW’s WindowSizeCallback to avoid our image getting stretched when we resize the window. Again, we’ll make use of an IORef to store the calculated projection matrix so that we can access it from the render loop. We’ll cover calculateProjectionMatrix later; for now on just assume it’s a function which takes a tuple of (width, height) and returns the projection matrix we need for that aspect ratio.

>         dims ← GLFW.getWindowSize win

>         projectionMatrix ← newIORef $

>           calculateProjectionMatrix dims

We’ll look into the details of what resize does later, but for now we just tell GLFW to call it when the window is resized. Since I don’t want to have any GLFW-specific code in the main portion of this demo, I drop the GLFW.Window parameter using const (I actually did the same for the WindowCloseCallback above, too).

>         GLFW.setWindowSizeCallback win $

>           Just (const $ resize projectionMatrix)

Let’s also make a quick helper function which swaps the draw buffers for the current window, so we don’t have to expose win to the rest of the program. We also put in a call to GLFW.pollEvents while we’re at it, so that window events and keypresses (if there were any) are handled properly.

>         let swapper = GLFW.swapBuffers win ≫ GLFW.pollEvents

That pretty much covers it for GLFW’s setup – we’re now ready to initialise and run our demo. We’ll have our main function just drop out when it’s done, so we can terminate once it’s complete.

>         initialise ≫= runDemo closed projectionMatrix swapper

>         GLFW.terminate

One last thing before I leave GLFW aside entirely – I’ll want to be able to access the time delta within my main loop. GLFW provides us with a convenient way to query this in a platform-agnostic manner.

> getDeltaTime :: IO GLfloat

> getDeltaTime = do

>   t ← GLFW.getTime

>   GLFW.setTime 0

>   return $ maybe 0 (fromRational ∘ toRational) t

This very simple implementation obviously assumes we will only be querying the delta time once per frame.

We now have a window set up and all the platform-specific stuff we might want handled. There’s just one more thing we need to get out of the way before we can begin looking at the actual GL side of things and the gl package in particular.

Constructing our cube mesh

We’re going to construct our mesh in code to avoid having to worry about model formats and so forth. This section has little to do with actual GL code, so if you’re keen to see the gl library in action you can safely skip it.

A mesh can be thought of as simply a collection of vertex data, and a set of indices into that data. For this demo, the information we need about each vertex is:

1. Its position relative to the model
2. Its colour
3. Its texture co-ordinates (Called UV Co-ordinates)
4. Its normal vector

We can store these in a structure with a Vector for each piece of data, along with an index Vector.

> data MeshSpec = MeshSpec

>   { specPositions 

:: 

V.Vector (V3 GLfloat)

>   , specColours   

:: 

V.Vector (V3 GLfloat)

>   , specNormals   

:: 

V.Vector (V3 GLfloat)

>   , specUVs       

:: 

V.Vector (V2 GLfloat)

>   , specIndices   

:: 

V.Vector (GLuint, GLuint, GLuint)

>   }

We’re going to be defining a lot of these values all at once. Unfortunately, this starts to look pretty ugly in Haskell because negative numbers have to be wrapped in brackets, so that the vector \((0, -1, 0)\) is expressed V3 0 (-1) 0. To try and ease the pain here, let’s define an alternate constructor for V3 values which takes a tuple instead of three parameters.

> v3 :: (a, a, a) → V3 a

> v3 (x, y, z) = V3 x y z

This allows us to define a function to generate a cuboid of any dimension. The function will take the dimensions of the cuboid and fill a MeshSpec with the required data.

> cuboid :: GLfloat → GLfloat → GLfloat → MeshSpec

> cuboid l' h' d' =

>   MeshSpec positions colours normals uvs indices where

>     l = l' * 0.5; d = d' * 0.5; h = h' * 0.5

I named my input parameters l', h', and d' because although I take the length, height, and depth as input, I generally want to use these values halved, so that I can treat them as an offset from the origin in the centre of the cuboid. These halved values, then, I give the more accessible names of l, h, and d. Here’s how I use them to define a quad for each face of the cube:

>     positions =

>       [v3 ( l, h, d), v3 ( l,-h, d), v3 ( l,-h,-d), v3 ( l, h,-d),

>        v3 ( l, h,-d), v3 (-l, h,-d), v3 (-l, h, d), v3 ( l, h, d),

>        v3 (-l, h, d), v3 (-l,-h, d), v3 ( l,-h, d), v3 ( l, h, d),

>        v3 (-l, h,-d), v3 (-l,-h,-d), v3 (-l,-h, d), v3 (-l, h, d),

>        v3 ( l,-h,-d), v3 ( l,-h, d), v3 (-l,-h, d), v3 (-l,-h,-d),

>        v3 ( l, h,-d), v3 ( l,-h,-d), v3 (-l,-h,-d), v3 (-l, h,-d)]

Each line here is a single face: The right, top, front, left, bottom and back faces respectively. I’m going to colour them so that the \((r, g, b)\) values are mapped to the (normalised) \((x, y, z)\) values. So the left, bottom, back point \((-l, -h, -d)\) is black, the right, bottom, back point \((l, -h, -d)\) is red, the right, top, front point \((l, h, d)\) is white… and so forth. This can be done by saying that for a particular point \((x, y, z)\) its RGB value can be calculated thus:

\[ \left(\frac{x + l}{l'}, \frac{y + h}{h'}, \frac{z + d}{d'}\right) \]

This can be expressed quite succinctly in Haskell.

>     colours = V.map ((/ V3 l' h' d') ∘ (+ V3 l h d)) positions

For the normals, we can simply take the normal vector for each axis, and the negations of those vectors. Since each face is composed of four vertices, and we want to share the same normal vector across the face, we replicate each normal four times – one for each vertex.

>     normals = V.concat ∘ map (V.replicate 4) $ ns ++ negated ns

>       where ns = [V3 1 0 0, V3 0 1 0, V3 0 0 1]

The texture co-ordinates for this shape are quite simple – they simply stretch from \((0, 0)\) in the bottom-left corner to \((1, 1)\) in the top-right. We want the same set of co-ordinates across each face, which again we can do using replicate.

>     uvs = V.concat ∘ replicate 6 $

>       [V2 0 0, V2 0 1, V2 1 1, V2 1 0]

Finally we set up the indices for our shape. The quads we defined in positions above follow a regular pattern: \((0, 1, 2, 3)\), \((4, 5, 6, 7)\)… essentially we just make a 4-tuple of incrementing numbers from an offset of \(faceIndex \times 4\).

>     indices =

>       quads ∘ V.zipWith forFace [0..] ∘ V.replicate 6 $ (0, 1, 2, 3)

>       where

>         

forFace i (a, b, c, d) = (a + i*4, b + i*4, c + i*4, d + i*4)

OpenGL doesn’t work with quads, though, it uses triangles. The quads function we just used takes the quads and splits them up into triangles.

>         

quads                    

= 

V.concatMap triangulate

>         

triangulate (a, b, c, d) 

= 

[(a, b, c), (c, d, a)]

…and that gives us the MeshSpec for our cube!

Considering each of these sets of vertex data separately is convenient when constructing the mesh, especially when you’re hard-coding like I did here. You’ll get better performance, though, if you combine them into a single, interleaved array (at least if you’re not deforming or otherwise modifying the mesh). This would just be a flat stream of GLfloats, like this:

  x1, y1, z1, r1, g1, b1, nx1, ny1, nz1, u1, v1, x2, y2, z2, r2, g2...

The indices are also represented as a flat list, an unpacked version of the tuple representation we use in MeshSpec above. The following type gives a representation closer to what we’d like to feed to GL.

> data MeshData = MeshData

>   { vertexData 

:: V.Vector GLfloat

>   , indexData  

:: V.Vector GLuint

>   }

Unpacking the indices to fit into the above structure is reasonably simple.

> unpackIndices 

:: 

V.Vector (GLuint, GLuint, GLuint)

>               

→ 

V.Vector GLuint

> unpackIndices = V.concatMap unpack

>   where unpack (a, b, c) = [a, b, c]

Interleaving the vertex data isn’t too much harder thanks to zipWith4.

> interleave 

:: 

V.Vector (V3 GLfloat)

>            

→ 

V.Vector (V3 GLfloat)

>            

→ 

V.Vector (V3 GLfloat)

>            

→ 

V.Vector (V2 GLfloat)

>            

→ 

V.Vector GLfloat

> interleave positions colours normals uvs =

>   V.foldr (V.++) V.empty $

>     V.zipWith4 combine positions colours normals uvs

>   where 

combine (V3 x y z) (V3 r g b) (V3 nx ny nz) (V2 u v) =

>         

  [x, y, z, r, g, b, nx, ny, nz, u, v]

Now we can use these functions to convert from a MeshSpec to a MeshData.

> fromMeshSpec :: MeshSpec → MeshData

> fromMeshSpec spec =

>   MeshData 

(interleave      

(specPositions spec)

>            

(specColours spec)

>            

(specNormals spec)

>            

(specUVs spec))

>            

(unpackIndices $

 specIndices spec)

This gets us from an easy-to-define “mesh specification” to the raw data that we’d like to give to GL. Here, we’ve defined the mesh in code, but you could just as well load the data from a file and read it into MeshData directly if you wanted.

Resource loading

OK, our basic setup is complete, it’s time to get down and dirty with OpenGL! First we need to load and prepare our resources.

Our aim here is to get a textured, spinning cube on the screen using modern OpenGL. To that end, the very least we will need is the texture, a shader program to do the rendering, and of course the mesh itself. Let’s define some datatypes to store these in.

First, the mesh. We use a Vertex Array Object to do the rendering, which contains references to all the data making up the mesh as well as settings describing the layout of the data (which parts of the stream to bind to which attributes in the shader).

The data itself is stored in Vertex Buffer Objects, which I have named VBO for the vertices and IBO for the indices. we bind these into the Vertex Array Object, so we don’t actually need them for rendering, but we keep hold of them for cleanup later.

More information on Vertex Buffer Objects and Vertex Array Objects can be found on the OpenGL wiki.

> data Mesh = Mesh

>   { meshVBO        

:: GLuint

>   , meshIBO        

:: GLuint

>   , meshVAO        

:: GLuint

>   , meshIndexCount 

:: GLsizei

>   }

For the shader, We want the ID for the shader program, and alongside that we’ll store the locations of all the constants and attributes. These will be different per-shader, but since in this case we only have one shader we can just assume they’ll always be the same.

> data Shader = Shader

>   { shaderProgram   

:: GLuint

>   , positions       

:: GLuint

>   , colours         

:: GLuint

>   , normals         

:: GLuint

>   , uvs             

:: GLuint

>   , pvmMatrix       

:: GLint

>   , viewModelMatrix 

:: GLint

>   , normalMatrix    

:: GLint

>   , diffuseColour   

:: GLint

>   , ambientColour   

:: GLint

>   , specularColour  

:: GLint

>   , shininess       

:: GLint

>   , lightDirection  

:: GLint

>   , diffuseMap      

:: GLint

>   }

This represents all the data we need to send to our shader. Note that contained within this structure are not the actual values (the positions, colours, matrices, etc), but the location at which the values are stored in the shader program. We’ll use these locations to set the values when we draw.

Finally, there’s the texture, which is simple – just the ID GL uses to refer to the texture is enough.

> type TextureID = GLuint

Packaging these two structures together , we create a Resources type representing all the resources this demo requires.

> data Resources = Resources

>   { mesh    

:: Mesh

>   , texture 

:: TextureID

>   , shader  

:: Shader

>   }

The job of our Initialise function, then, will be to load these resources and initialise them ready for use by GL. Loading and preparing resources for usage by GL may fail at any point, so I’m going to wrap the entire process in the MaybeT monad transformer so it drops out early on failure.

> initialise :: IO (Maybe Resources)

> initialise = runMaybeT $ do

Loading the texture

First let’s set up the texture. Here’s the texture we’re going to use; you can download it if you’re following along.

Loading the data is very simple. As it happens, I know that this image is an ImageRGBA8, so that’s all I’m going to handle – in reality you may need to handle various pixel formats depending on your input data.

>   png ← liftIO $ readPng "haskell.png"

>   (Image texWidth texHeight texData) ← MaybeT $ case png of

>     (Right (ImageRGBA8 i)) 

→ return $ Just i

>     (Left s)               

→ liftIO (print s) ≫ return Nothing

>     _                      

→ return Nothing

We now have the raw pixel buffer data for the texture. All that remains is to pass it to GL. First we generate the texture name which we’ll use to refer to it (although GL calls these “names”, it is just a GLuint ID, really).

>   textureID ← liftIO ∘ alloca $ \texIDPtr → do

>     glGenTextures 1 texIDPtr

>     peek texIDPtr

The idiom of allocating a temporary variable, passing it to GL to be filled, and then returning the filled value doesn’t feel very “Haskelly”, but it is exactly what GL expects. It means that when following along with a GL tutorial intended for C, you can pretty much switch the syntax and the examples will all work.

Writing out these three lines does get old pretty fast though, so let’s define a utility function which simplifies it. The following function assumes that the variable to be filled is the last one passed to the function.

>   let fillWith f = liftIO ∘ alloca $ liftM2 (≫) f peek

Now we have the texture name we can use it to bind and set up the texture. We use unsafeWith to get access to the raw pixel data from the Vector.

>   glBindTexture   GL_TEXTURE_2D textureID

>   let (w, h) = (fromIntegral texWidth, fromIntegral texHeight)

>   liftIO ∘ SV.unsafeWith texData $

>     glTexImage2D GL_TEXTURE_2D 0 GL_RGBA w h 0

>       GL_RGBA GL_UNSIGNED_BYTE ∘ castPtr

>   glTexParameteri GL_TEXTURE_2D

>     GL_TEXTURE_MAG_FILTER GL_LINEAR

>   glTexParameteri GL_TEXTURE_2D

>     GL_TEXTURE_MIN_FILTER GL_LINEAR

>   glTexParameteri GL_TEXTURE_2D

>     GL_TEXTURE_WRAP_S GL_CLAMP_TO_EDGE

>   glTexParameteri GL_TEXTURE_2D

>     GL_TEXTURE_WRAP_T GL_CLAMP_TO_EDGE

Loading the shaders

Next up are the shaders. The shader code itself is included at the end of this post; For now let’s just assume they are loaded into vertexShader.glsl and fragmentShader.glsl respectively.

Loading and compiling the two shaders is basically identical, so let’s create a utility function to help us.

>   let loadAndCompileShader 

:: 

GLenum → FilePath

>                            

→ 

IO (Maybe GLuint)

>       loadAndCompileShader shaderType filename = do

First we request GL to create a shader object for us.

>         shaderID ← glCreateShader shaderType

After that we load the shader file and bind its contents to our new shader object. glShaderSource is looking for an array of C-style strings, or in other words a pointer to a pointer of GLchar, expressed in C as const GLchar**. This is where working at such a low level starts to get a bit fiddly in Haskell – you can certainly do it, but it’s not quite as succinct as it would be in C.

>         shaderCode ← T.readFile filename

>         T.withCStringLen shaderCode $

>           \(str, len) → with str $

>             \strPtr → with (fromIntegral len) $

>               \lenPtr → glShaderSource shaderID 1 strPtr lenPtr

Compare the four lines starting T.withCStringLen with the C equivalent:

    glShaderSource(shaderID, 1, &shaderCode, NULL);

Admittedly this isn’t an entirely fair comparison – it assumes NULL-terminated strings which we weren’t using in Haskell, and of course the file loading directly preceding it would have been more arduous in C. Still, the point stands that what is a simple operator in C (&) requires a call to with and a lambda function in Haskell.

    evalContT $ do

      (str, len) 

← ContT (T.withCStringLen shaderCode)

      strPtr     

← ContT (with str)

      lenPtr     

← ContT (with $ fromIntegral len)

      liftIO $ glShaderSource shaderID 1 strPtr lenPtr

    glShaderSource shaderID 1 <$> str <*> len

Anyway, now that the shader’s loaded into memory, our utility function can compile it and check that compilation succeeded.

>         glCompileShader shaderID

>         compileStatus ← fillWith $

>           glGetShaderiv shaderID GL_COMPILE_STATUS

If compilation failed, we output the info log to tell us what happened. We have to do a little bit of marshalling between C and Haskell datatypes to access the log as a Text object for printing.

>         when (compileStatus == GL_FALSE) $ do

>           infoLogLength ← fillWith $

>             glGetShaderiv shaderID GL_INFO_LOG_LENGTH

>           let infoLogLength' = fromIntegral infoLogLength

>           allocaBytes infoLogLength' $ \infoBuffer → do

>               glGetShaderInfoLog 

shaderID infoLogLength

>                                  

nullPtr infoBuffer

>               T.putStr =≪ 

T.peekCStringLen (

infoBuffer,

>                            

infoLogLength')

Having done that, we can return the ID of our compiled shader object if compilation was successful, or Nothing otherwise.

>         return $ 

if compileStatus == GL_TRUE

>                  

then Just shaderID else Nothing

Our helper function complete, let’s use it to load the vertex and fragment shaders. We wrap the calls to loadAndCompileShader in MaybeT so that this function will drop out automatically if either of them fail.

>   vs 

← 

MaybeT $ loadAndCompileShader

>      

  GL_VERTEX_SHADER "vertexShader.glsl"

>   fs 

← 

MaybeT $ loadAndCompileShader

>      

  GL_FRAGMENT_SHADER "fragmentShader.glsl"

Now we need to generate our shader program and link the two shader objects into it.

>   programID ← glCreateProgram

>   glAttachShader programID vs

>   glAttachShader programID fs

>   glLinkProgram  programID

>   linkStatus ← fillWith $

>     glGetProgramiv programID GL_LINK_STATUS

Here again we output the log and drop out of the initialisation with Nothing if linkStatus is GL_FALSE.

>   when (linkStatus == GL_FALSE) ∘ MaybeT $ do

>     infoLogLength ← fillWith $

>       glGetProgramiv programID GL_INFO_LOG_LENGTH

>     let infoLogLength' = fromIntegral infoLogLength

>     allocaBytes infoLogLength' $ \infoBuffer → do

>       glGetProgramInfoLog 

programID infoLogLength

>                           

nullPtr infoBuffer

>       T.putStr =≪ T.peekCStringLen (infoBuffer, infoLogLength')

>     return Nothing

Having linked the shader program, we can throw away the individual shader objects that went into it, which will make cleaning up later easier.

>   glDeleteShader vs

>   glDeleteShader fs

We now know that we have a valid, correctly linked program identified by programID. We can query this for the locations of its attributes and constants which we’ll use to set their values later.

To ease the marshalling between Haskell and C I’m going to define a couple of helper functions here. The first, unsign, takes the C idiom of returning negative numbers on failure and converts it into the Haskell Maybe type.

>   let unsign :: Integral a ⇒ GLint → Maybe a

>       unsign x 

| x < 0     

= Nothing

>                

| otherwise 

= Just $ fromIntegral x

The second helper function deals with marshalling strings to C. I’m going to use ContT to reduce the reliance on callback functions. The forString function will take in a function expecting a program ID and a C string, along with a Text object with the actual string we want to use. It will transform this into an action wrapped in ContT and MaybeT, representing the fact that it is run as part of a sequence of callbacks, any of which might fail, in which case they should all fail. Since we’re always going to be querying the same shader program we’ll just refer to it directly in fromString so that we don’t have to pass it in every time. Finally we use unsign to return Nothing on failure.

>   let forString 

:: 

Integral a

>                 

⇒ 

(GLuint → Ptr GLchar → IO GLint)

>                 

→ 

T.Text → MaybeT (ContT r IO) a

>       f `forString` x = do

>         (str, _) ← lift $

>           ContT (T.withCStringLen $ T.concat [x, "\0"])

>         loc ← liftIO $ f programID str

>         MaybeT ∘ return $ unsign loc

Armed with forString, what would have been a tedious process of marshalling C strings through a series of callbacks can be expressed quite idiomatically:

>   glShader ← MaybeT ∘ evalContT ∘ runMaybeT $

>     Shader

>       <$> pure programID

>       <*> glGetAttribLocation  

`forString` "position"

>       <*> glGetAttribLocation  

`forString` "colour"

>       <*> glGetAttribLocation  

`forString` "normal"

>       <*> glGetAttribLocation  

`forString` "uv"

>       <*> glGetUniformLocation 

`forString` "pvmMatrix"

>       <*> glGetUniformLocation 

`forString` "viewModelMatrix"

>       <*> glGetUniformLocation 

`forString` "normalMatrix"

>       <*> glGetUniformLocation 

`forString` "diffuseColour"

>       <*> glGetUniformLocation 

`forString` "ambientColour"

>       <*> glGetUniformLocation 

`forString` "specularColour"

>       <*> glGetUniformLocation 

`forString` "shininess"

>       <*> glGetUniformLocation 

`forString` "lightDirection"

>       <*> glGetUniformLocation 

`forString` "diffuseMap"

It is important that the names of the attributes and uniforms above match those that are actually used in the shaders, otherwise they won’t be found and we’ll drop out with Nothing here.

Loading the mesh

Finally, here’s the mesh. We’ll initialise a MeshSpec describing a \(1\times1\times1\) cube and convert that to MeshData using the functions described in the previous section. At that point we’ll have some raw data, such as might have been read in from a model file if we were drawing something more complicated than a cube.

>   let cube = fromMeshSpec $ cuboid 1 1 1

We need to create two buffer objects: our VBO and our IBO. We create buffer objects using glGenBuffers; this in turn will give as an ID for each buffer with which we can refer to it.

glGenBuffers takes an array and a length and fills the values in that array with that many buffers. We use the facilities in Foreign.Marshal.Array to allocate the array and pull out the values at the end.

>   [vbo, ibo] ← liftIO ∘ allocaArray 2 $ \buffers → do

>     glGenBuffers 2 buffers

>     peekArray 2 buffers

We’ll start by setting up the vertex buffer. First we need to bind the buffer ID we just got to the GL_ARRAY_BUFFER target so that GL knows what we intend to do with it. Then we fill it with data. Finally, we bind 0 to GL_ARRAY_BUFFER to free it up.

>   glBindBuffer GL_ARRAY_BUFFER vbo

>   let 

vertices   

= vertexData cube

>       

vertexBufSize 

= sizeOf (V.head vertices) * V.length vertices

>   liftIO ∘ SV.unsafeWith (SV.convert vertices) $ \vsPtr →

>     glBufferData 

GL_ARRAY_BUFFER

>                  

(fromIntegral vertexBufSize)

>                  

(castPtr vsPtr)

>                  

GL_STATIC_DRAW

>   glBindBuffer GL_ARRAY_BUFFER 0

Again we use unsafeWith to get the data into C. We have to convert the vector into a Storable vector using Data.Vector.Storable.convert before we can do this.

Setting up the index buffer is similar, only this time the target is GL_ELEMENT_ARRAY_BUFFER.

>   glBindBuffer GL_ELEMENT_ARRAY_BUFFER ibo

>   let 

indices   

= indexData cube

>       

indexBufSize 

= sizeOf (V.head indices) * V.length indices

>   liftIO ∘ SV.unsafeWith (SV.convert indices) $ \isPtr →

>     glBufferData 

GL_ELEMENT_ARRAY_BUFFER

>                  

(fromIntegral indexBufSize)

>                  

(castPtr isPtr)

>                  

GL_STATIC_DRAW

>   glBindBuffer GL_ELEMENT_ARRAY_BUFFER 0

Now that our buffer objects are set up for vertices and indices, we can wrap them up together in a Vertex Array Object. This collects the data together with properties about how it should be used. First we generate and bind the vertex array object, much as we did the vertex buffer objects earlier.

>   vao ← liftIO ∘ alloca $ \vaoPtr → do

>     glGenVertexArrays 1 vaoPtr

>     peek vaoPtr

>   glBindVertexArray vao

Next we bind the buffer objects we made for the vertex and index data to this new vertex array object.

>   glBindBuffer GL_ARRAY_BUFFER vbo

>   glBindBuffer GL_ELEMENT_ARRAY_BUFFER ibo

We need to enable all four of the attributes our shader uses.

>   glEnableVertexAttribArray (positions glShader)

>   glEnableVertexAttribArray (colours glShader)

>   glEnableVertexAttribArray (normals glShader)

>   glEnableVertexAttribArray (uvs glShader)

And finally, we fill in the attributes, which tells GL the actual layout of the data within the buffer. When talking about the layout, we’re mainly talking about two things: The offset and the stride. The offset tells us how far into the array that chunk of data begins, while the stride tells us the difference from the start of one set of values to the start of the next. Since we have all our data in one interleaved array, the stride will be the same for each kind of data: 11 * sizeof(GLfloat).

>   let 

offset x

= wordPtrToPtr $ x * fromIntegral floatSize

>       

stride    

= fromIntegral floatSize * 11

>       

floatSize 

= sizeOf (undefined::GLfloat)

Now we can set the values for each type using glVertexAttribPointer.

>   glVertexAttribPointer (positions glShader)

>     3 GL_FLOAT GL_FALSE stride (offset 0)

>   glVertexAttribPointer (colours glShader)

>     3 GL_FLOAT GL_FALSE stride (offset 3)

>   glVertexAttribPointer (normals glShader)

>     3 GL_FLOAT GL_FALSE stride (offset 6)

>   glVertexAttribPointer (uvs glShader)

>     2 GL_FLOAT GL_FALSE stride (offset 9)

Our buffer objects are now set up and loaded onto the GPU ready to use. The last thing to do is to put them in the Mesh structure ready to be added to our Resources.

>   let glMesh = Mesh vbo ibo vao (fromIntegral $ V.length indices)

Now that we have everything we need, we call initGL and then return the Resources.

>   liftIO initGL ≫ return (Resources glMesh textureID glShader)

And we’re done! Our Resources handle should now contain all the data we need, unless there was a problem, in which case we’ll fail gracefully.

Setting up GL

That call to initGL at the end of initialise allows us to give GL its basic settings.

> initGL :: IO ()

> initGL = do

>   glClearColor 

0.96 0.96 0.96 1

>   glClearDepth 

1

>   glEnable     

GL_DEPTH_TEST

>   glDepthFunc  

GL_LEQUAL

>   glCullFace   

GL_BACK

While we’re here, remember the resize function we gave to GLFW at the start? Let’s get the definition of that out of the way.

> resize :: IORef (M44 GLfloat) → Int → Int → IO ()

> resize projectionMatrix w h = do

resize takes the IORef we made to store the projection matrix, and the new width and height. It has two jobs: it needs to update the viewport, so that GL rendering can fill the window, and it needs to update the projection matrix, so that the aspect ratio doesn’t get ruined.

Setting the viewport is simple – just pass the origin (0, 0), and the full width and height of the window. Of course. if we only wanted to draw into a subset of the window that’s what we’d pass. The projection matrix is calculated using the same function we used in main: calculateProjectionMatrix. It is then written to the IORef so that we can access it from within our main loop.

>   glViewport 0 0 (fromIntegral w) (fromIntegral h)

>   writeIORef projectionMatrix $ calculateProjectionMatrix (w, h)

Here’s the calculateProjectionMatrix function itself. We use the perspective function from linear to do the work for us. π/3 radians gives us a field of view of 60°.

> calculateProjectionMatrix :: Integral a ⇒ (a, a) → M44 GLfloat

> calculateProjectionMatrix (w, h) =

>   perspective (π/3) (fromIntegral w / fromIntegral h) 1 100

Handling state

This demo is very simple, so there isn’t much state to deal with. Nevertheless, the cube does spin, so we will need to keep track of its angle. As well as that, I’m going to include the camera position within the state structure even though it remains constant throughout the demo, as it’s convenient to hold the data together, and in real life you’re almost certainly going to be moving the camera at some point anyway.

Our state, then, can be represented as follows:

> data DemoState = DemoState

>   { cubeRotation   

:: 

Quaternion GLfloat

>   , cameraPosition 

:: 

V3 GLfloat

>   }

And the default state is simply:

> defaultState :: DemoState

> defaultState = DemoState

>   { cubeRotation   

= 

axisAngle (V3 0 1 0) 0

>   , cameraPosition 

= 

V3 0 1 (-2)

>   }

There are a number of ways to handle varying state in Haskell, and which to use is an interesting choice which can have wide-reaching implications for your application. For this demo, though, I’m keeping it simple, as I want to keep the focus on use of the gl library. So we’ll just have a simple update function which takes the previous state and a time delta, and returns the new state.

> update :: DemoState → GLfloat → DemoState

> update s dt =

>   s { cubeRotation = cubeRotatedBy (rotationSpeed * dt) }

>   where

>     cubeRotatedBy θ 

= 

cubeRotation s * axisAngle (V3 0 1 0) θ

>     rotationSpeed   

= 

π / 2

The main loop

Our runDemo function will comprise the main loop for this demo. It takes the two IORefs we created at the start, a callback we can use to swap the framebuffers, and the Resources we just loaded. If the resources failed to load it just drops out straight away.

> runDemo 

:: 

IORef Bool

>         

→ 

IORef (M44 GLfloat)

>         

→ 

IO ()

>         

→ 

Maybe Resources

>         

→ 

IO ()

> runDemo _ _ _ Nothing = return ()

Otherwise it runs loop, which runs the frame unless the value pointed to by closed is True. When it is True, loop drops out and cleanup gets run.

> runDemo closed projectionMatrix swapBuffers (Just res) =

>   do 

loop defaultState

>      

cleanup res where

>   loop s = readIORef closed ≫= \c → unless c (runFrame s)

The frame itself is comprised of essentially two phases, the update and the draw phase. We pass the delta time value to the update, but not the draw. Finally we call loop, which again checks closed and runs the next frame.

>   runFrame s = do

>     draw res s =≪ readIORef projectionMatrix

>     glFlush ≫ swapBuffers

>     dt ← getDeltaTime

>     loop $ update s dt

Actually drawing things

At long last, we’re ready to implement the draw function, which actually renders the graphics to the screen. This function is actually surprisingly simple. A lot of the work in graphics programming goes into efficiently moving data between the CPU and the GPU – that and the shader code, of course. The actual rendering part is doing little more than passing constants to the shader to work with.

> draw :: Resources → DemoState → M44 GLfloat → IO ()

> draw res state projectionMatrix = do

Note that we are taking the projection matrix directly here, rather than the IORef. We let the main loop deal with the fact that this might be modified in a callback – as far as the draw function is concerned, this is the projection matrix it is dealing with and it will not change – not during this frame, at least.

We have the projection matrix, but there are a number of other matrices we’ll need to calculate. The view matrix offsets everything based on the position of the camera. The model matrix then applies the model transformations (in this case just rotation).

>   let 

viewMat =

>       

  lookAt (cameraPosition state) (V3 0 0 0) (V3 0 1 0)

>       

modelMat =

>       

  mkTransformation (cubeRotation state) (V3 0 0 0)

It is convenient to precalculate the products of these matrices.

>       

viewModelMat 

= viewMat !*! modelMat

>       

pvmMat       

= projectionMatrix !*! viewModelMat

Finally the normal matrix is used to interpolate normals across faces. Since not all matrices have a valid inverse, I’ve chosen to fall back on the identity matrix in case inv33 returns Nothing.

>       

viewModelMat33 

= viewModelMat ^. _xyz . column _xyz

>       

inverseMat     

= inv33 viewModelMat33

>       

normalMat      

= maybe identity distribute inverseMat

Now we have all the data we need, we can start sending it to GL. We start by clearing both the colour and the depth buffers.

>   glClear 

 $  

GL_COLOR_BUFFER_BIT

>           

.|. 

GL_DEPTH_BUFFER_BIT

Next, we bind the shader program, mesh, and texture ready for use. The texture is bound to texture unit 0, which will become important in a minute.

>   glUseProgram ∘ shaderProgram $ shader res

>   glBindVertexArray ∘ meshVAO $ mesh res

>   glActiveTexture GL_TEXTURE0

>   glBindTexture GL_TEXTURE_2D $ texture res

We pass in the required uniforms to the shader. First the matrices, where the Storable instance for M44 helps us a lot.

>   with pvmMat $

>     glUniformMatrix4fv 

(pvmMatrix $ shader res)

>                        

1 GL_TRUE ∘ castPtr

>   with viewModelMat $

>     glUniformMatrix4fv 

(viewModelMatrix $ shader res)

>                        

1 GL_TRUE ∘ castPtr

>   with normalMat $

>     glUniformMatrix3fv 

(normalMatrix $ shader res)

>                        

1 GL_TRUE ∘ castPtr

And the light and texture data, which is simple. For the texture, the number passed is the index of the texture unit that texture is bound to; we specified GL_TEXTURE0 a minute ago so we put 0 here.

>   glUniform4f (diffuseColour $ shader res)  

0.6 0.6 0.6 1

>   glUniform4f (ambientColour $ shader res)  

0.1 0.1 0.1 1

>   glUniform4f (specularColour $ shader res) 

0.7 0.7 0.7 1

>   glUniform1f (shininess $ shader res)      

0.4

>   glUniform3f (lightDirection $ shader res) 

0 0 1

>   glUniform1i (diffuseMap $ shader res)     

0

Finally, we’re ready to draw!

>   glDrawElements 

GL_TRIANGLES

>                  

(meshIndexCount $ mesh res)

>                  

GL_UNSIGNED_INT

>                  

(wordPtrToPtr 0)

If you’ve got this far you should have a spinning cube on the screen! Pat yourself on the back; you’re ready to go.

Resource cleanup

OK, we’ve had our fun, now we need to clean up after ourselves. Actually, since we’re on our way out of the application we don’t as the OS will no doubt take care of it for us, but I’m going to anyway for the sake of completeness if nothing else.

> cleanup :: Resources → IO ()

> cleanup (Resources m t s) = do

>   with (meshVAO m) 

$ glDeleteVertexArrays 1

>   with (meshVBO m) 

$ glDeleteBuffers 1

>   with (meshIBO m) 

$ glDeleteBuffers 1

>   with t           

$ glDeleteTextures 1

>   glDeleteProgram  

$ shaderProgram s

The gist of this is pretty simple: for every glCreate* or glGen* function there is a glDelete* equivalent which we have to call.

Final thoughts

Whew, well, that was a pretty long post! I hope that it will come in handy for anyone who, like me, wants to fiddle about with OpenGL in Haskell but doesn’t want to spend hours getting the basic pipeline up and running. Obviously you will want to build your own abstractions on top of this and presumably draw something more interesting than a rubbish cube. But at least with this as a starting point you’ll be able to build it up from a program that works.

If you liked this post, please drop me a tweet @danielpwright! If it’s popular, I might explore some other libraries in a similar way. Similarly, if you found anything lacking, please let me know.

As I mentioned, this was also my first time using the gl library. Having played with it a bit now, I must say that I like it, despite the annoyance of having to marshal data into C manually. This process is quite easy to abstract into something easier to use, and if it’s me doing the abstraction I can be sure it will be well-suited to my application.

Apart from that, coming from a traditional games background (my day job is as a console games programmer in C++), we tend to be quite obssessive over what our memory is doing. Even having garbage collection feels a bit… free and easy, let alone all the other high-level constructs Haskell offers! Knowing that I’m dealing with raw GL bindings and being able to see exactly how data is marshalled between Haskell and C gives me a reassuring sense that, at least as far as my graphics pipeline is concerned, I am in control of my data. There’s nothing worse than getting a little way into something and then realising that something you hadn’t anticipated about the abstraction you’re working with prevents you from doing the thing you want to do.

There is probably still a place for a package like OpenGL. The level of abstraction there feels much more natural for a Haskell library. But I think, for my part, I’d rather set the level of abstraction myself, so as to best match the needs of the project I’m working on, so I will be using the gl package for any graphics projects I do from now on.

Appendix: shader code

Here is the code for the two shaders I use in this demo. They are cobbled together from a variety of tutorials on the internet, and aren’t really very useful for any sort of production use, given that they only allow for a single directional light, they assume coloured vertices and alpha-blended textures, and so on. The goal here wasn’t really to explore interesting shader code or graphics techniques, but rather to give an absolute baseline working environment in GL.

So, I assume that once you have this up and running one of the first things you’ll want to do is throw away these shaders and replace them with something more useful, possibly by following one of the many tutorials on the internet for working with OpenGL in C/C++, since the code samples translate quite naturally when using the gl package.

I include these two shaders, therefore, without comment.

vertexShader.glsl

 #version 330

uniform mat4 pvmMatrix;

uniform mat4 viewModelMatrix;

uniform mat3 normalMatrix;

in vec3 position;

in vec3 colour;

in vec3 normal;

in vec2 uv;

out vec3 calculatedNormal;

out vec4 calculatedEye;

out vec4 rgba;

out vec2 fragmentUV;

void main ()

{

  vec4 position4 = vec4(position, 1.0);

  gl_Position = pvmMatrix * position4;

  calculatedNormal = normalize(normalMatrix * normal);

  calculatedEye = -(viewModelMatrix * position4);

  rgba = vec4(colour, 1.0);

  fragmentUV = uv;

}

fragmentShader.glsl

 #version 330

uniform vec4 diffuseColour;

uniform vec4 ambientColour;

uniform vec4 specularColour;

uniform float shininess;

uniform vec3 lightDirection;

uniform sampler2D diffuseMap;

in vec3 calculatedNormal;

in vec4 calculatedEye;

in vec4 rgba;

in vec2 fragmentUV;

out vec4 colorOut;

void main()

{

    vec4 spec = vec4(0.0);

    vec3 n = normalize(calculatedNormal);

    float intensity = max(dot(n,lightDirection), 0.0);

    if (intensity > 0.0)

    {

        vec3 e = normalize(vec3(calculatedEye));

        vec3 h = normalize(lightDirection + e);

        float intSpec = max(dot(h,n), 0.0);

        spec = specularColour * pow(intSpec,shininess);

    }

    vec4 texCol = texture(diffuseMap, fragmentUV);

    vec4 baseCol = mix(rgba, texCol, texCol.a);

    colorOut = baseCol * max(intensity * diffuseColour + spec, ambientColour);

}